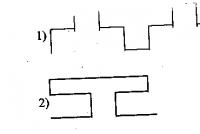
Примеры индукции. Метод математической индукции: примеры решения

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Введение

Данная тема является актуальной, так как каждый день люди решают различные задачи, в которых они применяют разные методы решения, но есть задания, в которых не обойтись без метода математической индукции, и в таких случаях будут очень полезны знания в данной области.

Я выбрал данную тему для исследования, потому что в школьной программе методу математической индукции уделяют мало времени, ученик узнает поверхностнуюинформацию, которая поможетему получить лишь общее представление о данном методе, но чтобы углубленно изучить эту теорию потребуется саморазвитие. Действительно будет полезно поподробнее узнать о данной теме, так как это расширяет кругозор человека и помогает в решении сложных задач.

Цель работы:

Познакомиться с методом математической индукции, систематизировать знания по данной теме и применить её при решении математических задач и доказательстве теорем, обосновать и наглядно показать практическое значение метода математической индукции как необходимого фактора для решения задач.

Задачи работы:

Проанализировать литературу и обобщить знания по данной теме.

Разобраться в принципе метода математической индукции.

Исследовать применение метода математической индукции к решению задач.

Сформулировать выводы и умозаключения по проделанной работе.

Основная часть исследования

История возникновения:

Только к концу XIX века сложился стандарт требований к логической строгости, остающейся и до настоящего времени господствующими в практической работе математиков над развитием отдельных математических теорий.

Индукция - познавательная процедура, посредством которой из сравнения наличных фактов выводится обобщающее их утверждение.

В математике роль индукции в значительной степени состоит в том, что она лежит в основе выбираемой аксиоматики. После того как длительная практика показала, что прямой путь всегда короче кривого или ломанного, естественно было сформулировать аксиому: для любых трех точек А, В и С выполняется неравенство.

Осознание метода математической индукции как отдельного важного метода восходит к Блезу Паскалю и Герсониду, хотя отдельные случаи применения встречаются ещё в античные времена у Прокла и Эвклида. Современное название метода было введено де Морганом в 1838 году.

Метод математической индукции можно сравнить с прогрессом: мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению логически развивать свою мысль, а значит, сама природа предначертала ему размышлять индуктивно.

Индукция и дедукция

Известно, что существуют как частные, так и общие утверждения, и на переходе от одних к другим и основаны два данных термина.

Дедукция (от лат. deductio - выведение) - переход в процессе познания от общего знания к частному и единичному . В дедукции общее знание служит исходным пунктом рассуждения, и это общее знание предполагается «готовым», существующим. Особенность дедукции состоит в том, что истинность ее посылок гарантирует истинность заключения. Поэтому дедукция обладает огромной силой убеждения и широко применяется не только для доказательства теорем в математике, но и всюду, где необходимы достоверные знания.

Индукция (от лат. inductio - наведение) - это переход в процессе познания от частного знания к общему .Другими словами, - это метод исследования, познания, связанный с обобщением результатов наблюдений и экспериментов.Особенностью индукции является ее вероятностный характер, т.е. при истинности исходных посылок заключение индукции только вероятно истинно и в конечном результате может оказаться как истинным, так и ложным.

Полная и неполная индукция

Индуктивное умозаключение - такая форма абстрактного мышления, в которой мысль развивается от знания меньшей степени общности к знанию большей степени общности, а заключение, вытекающее из посылок, носит преимущественно вероятностный характер.

В ходе исследования я выяснил, что индукция делится на два вида: полная и неполная.

Полной индукцией называется умозаключение, в котором общий вывод о классе предметов делается на основании изучения всех предметов этого класса.

Например,пусть требуется установить, что каждое натуральное чётное число n в пределах 6≤ n≤ 18 представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения:

6=3+3; 8=5+3; 10=7+3; 12=7+5;14=7+7; 16=11+5; 18=13+5;

Данные равенства показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.

Рассмотрим следующий пример: последовательность yn= n 2 +n+17; Выпишем первые четыре члена: у 1 =19; y 2 =23; y 3 =29; y 4 =37; Тогда мы можем предположить, что вся последовательность состоит из простых чисел. Но это не так, возьмем y 16 = 16 2 +16+17=16(16+1)+17=17*17. Это составное число, значит наше предположение неверно, таким образом, неполная индукция не приводит к вполне надежным выводам, но позволяет сформулировать гипотезу, которая в дальнейшем требует математического доказательства или опровержения.

Метод математической индукции

Полная индукция имеет в математике лишь ограниченное применение. Многие интересные математические утверждения охватывают бесконечное число частных случаев, а провести проверку для всех этих ситуаций мы не в состоянии.Но как осуществить проверку бесконечного числа случаев? Такой способ предложили Б.Паскаль и Я.Бернулли, это метод математической индукции, в основе которого лежит принцип математической индукции .

Если предложение А(n), зависящее от натурального числа n, истинно для n=1 и из того, что оно истинно для n=k (где k-любое натуральное число), следует, что оно истинно и для следующего числа n=k+1, то предположение А(n) истинно для любого натурального числа n.

Если предложение А(n) истинно при n=p и если А(k) А(k+1) для любого k>p, то предложение А(n) истинно для любого n>p.

Алгоритм (он состоит из четырех этапов):

1.база (показываем, что доказываемое утверждение верно для некоторых простейших частных случаев (п = 1));

2.предположение (предполагаем, что утверждение доказано для первых к случаев); 3 .шаг (в этом предположении доказываем утверждение для случая п = к + 1); 4.вывод (у тверждение верно для всех случаев, то есть для всех п) .

Заметим, что Методом математической индукции можно решать не все задачи, а только задачи, параметризованные некоторой переменной. Эта переменная называется переменной индукции.

Применение метода математической индукции

Применим всю данную теорию на практике и выясним, в каких задачах применяется данный метод.

Задачи на доказательство неравенств.

Пример 1. Доказать неравенство Бернулли(1+х)n≥1+n х, х>-1, n € N.

1) При n=1 неравенство справедливо, так как 1+х≥1+х

2) Предположим, что неравенство верно для некоторого n=k, т.е.

(1+х) k ≥1+k x.

Умножив обе части неравенства на положительное число 1+х, получим

(1+x) k+1 ≥(1+kx)(1+ x) =1+(k+1) x + kx 2

Учитывая, что kx 2 ≥0, приходим к неравенству

(1+х) k+1 ≥1+(k+1) x.

Таким образом, из допущения, что неравенство Бернулли верно для n=k, следует, что оно верно для n=k+1. На основании метода математической индукции можно утверждать, что неравенство Бернулли справедливо для любого n € N.

Пример 2. Доказать, что при любом натуральном n>1, .

Докажем с помощью метода математической индукции.

Обозначим левую часть неравенства через.

1), следовательно, при n=2 неравенство справедливо.

2)Пусть при некоторомk. Докажем, что тогда и. Имеем, .

Сравнивая и, имеем, т.е. .

При любом натуральном k правая часть последнего равенства положительна. Поэтому. Но, значит, и.Мы доказали справедливость неравенства при n=k+1, следовательно, в силу метода математической индукции, неравенство справедливо для любого натурального n>1.

Задачи на доказательство тождеств.

Пример 1. Доказать, что для любого натурального n справедливо равенство:

1 3 +2 3 +3 3 +…+n 3 =n 2 (n+1) 2 /4.

Пусть n=1, тогда Х 1 =1 3 =1 2 (1+1) 2 /4=1.

Мы видим, что при n=1 утверждение верно.

2) Предположим, что равенство верно при n=kX k =k 2 (k+1) 2 /4.

3) Докажем истинность этого утверждения для n=k+1, т.е.X k+1 =(k+1) 2 (k+2) 2 /4. X k+1 =1 3 +2 3 +…+k 3 +(k+1) 3 =k 2 (k+1) 2 /4+(k+1) 3 =(k 2 (k+1) 2 +4(k+1) 3)/4=(k+1) 2 (k 2 +4k+4)/4=(k+1) 2 (k+2) 2 /4.

Из приведённого доказательства видно, что утверждение верно при n=k+1, следовательно, равенство верно при любом натуральном n.

Пример 2. Доказать, что при любом натуральном nсправедливо равенство

1) Проверим, что это тождество верно приn = 1.; - верно.

2) Пусть тождество верно и для n = k, т.е..

3)Докажем, что это тождество верно и для n = k + 1, т.е.;

Т.к. равенство верно при n=kи n=k+1, то оно справедливо при любом натуральном n.

Задачи на суммирование.

Пример 1. Доказать, что 1+3+5+…+(2n-1)=n 2 .

Решение: 1) Имеем n=1=1 2 . Следовательно, утверждение верно при n=1, т.е. А(1) истинно.

2) Докажем, что А(k) A(k+1).

Пусть k-любое натуральное число и пусть утверждение справедливо для n=k, т.е.1+3+5+…+(2k-1)=k 2 .

Докажем, что тогда утверждение справедливо и для следующего натурального числа n=k+1, т.е. что

1+3+5+…+(2k+1)=(k+1) 2 .

В самом деле,1+3+5+…+(2k-1)+(2k+1)=k 2 +2k+1=(k+1) 2 .

Итак, А(k) А(k+1). На основании принципа математической индукции заключаем, что предположение А(n) истинно для любого n N.

Пример 2. Доказать формулу, n - натуральное число.

Решение: При n=1 обе части равенства обращаются в единицу и, следовательно, первое условие принципа математической индукции выполнено.

Предположим, что формула верна при n=k, т.е. .

Прибавим к обеим частям этого равенства и преобразуем правую часть. Тогда получим

Таким образом, из того, что формула верна при n=k, следует, что она верна и при n=k+1, то это утверждение справедливо при любом натуральном n.

Задачи на делимость.

Пример 1. Доказать, что (11 n+2 +12 2n+1) делится на 133 без остатка.

Решение: 1) Пусть n=1, тогда

11 3 +12 3 =(11+12)(11 2 -132+12 2)=23× 133.

(23× 133) делится на 133 без остатка, значит при n=1 утверждение верно;

2) Предположим, что (11 k+2 +12 2k+1) делится на 133 без остатка.

3) Докажем, что в таком случае

(11 k+3 +12 2k+3) делится на 133 без остатка. Действительно, 11 k+3 +12 2л+3 =11×11 k+2 +

12 2 ×12 2k+1 =11× 11 k+2 +(11+133)× 12 2k+1 =11(11 k+2 +12 2k+1)+133× 12 2k+1 .

Полученная сумма делится на 133 без остатка, так как первое её слагаемое делится на 133 без остатка по предположению, а во втором одним из множителей является 133.

Итак, А(k)→ А(k+1), то опираясь на метод математической индукции, утверждение верно для любых натуральных n.

Пример 2. Доказать, что 3 3n-1 +2 4n-3 при произвольном натуральном n делится на 11.

Решение: 1) Пусть n=1, тогдаХ 1 =3 3-1 +2 4-3 =3 2 +2 1 =11 делится на 11 без остатка. Значит, при n=1 утверждение верно.

2) Предположим, что при n=k

X k =3 3k-1 +2 4k-3 делится на 11 без остатка.

3) Докажем, что утверждение верно для n=k+1.

X k+1 =3 3(k+1)-1 +2 4(k+1)-3 =3 3k+2 +2 4k+1 =3 3 *3 3k-1 +2 4 *2 4k-3 =

27 3 3k-1 +16* 2 4k-3 =(16+11)* 3 3k-1 +16* 2 4k-3 =16* 3 3k-1 +

11* 3 3k-1 +16* 2 4k-3 =16(3 3k-1 +2 4k-3)+11* 3 3k-1 .

Первое слагаемое делится на 11 без остатка, поскольку 3 3k-1 +2 4k-3 делится на 11 по предположению, второе делится на 11, потому что одним из его множителей есть число 11. Значит и сумма делится на 11 без остатка при любом натуральном n.

Задачи из реальной жизни.

Пример 1. Доказать, что сумма Sn внутренних углов любого выпуклого многоугольника равна (п - 2)π, где п — число сторон этого многоугольника:Sn = (п - 2)π (1).

Это утверждение имеет смысл не для всех натуральных п , а лишь для п > 3, так как минимальное число углов в треугольнике равно 3.

1) При п = 3 наше утверждение принимает вид: S 3 = π. Но сумма внутренних углов любого треугольника действительно равна π. Поэтому при п = 3 формула (1) верна.

2) Пусть эта формула верна при n=k , то есть S k = (k - 2)π, где k > 3. Докажем, что в таком случае имеет место и формула:S k+ 1 = (k - 1)π.

Пусть A 1 A 2 ... A k A k+ 1 —произвольный выпуклый (k + 1) -угольник (рис. 338).

Соединив точки A 1 и A k , мы получим выпуклый k -угольник A 1 A 2 ... A k — 1 A k . Очевидно, что сумма углов (k + 1) -угольника A 1 A 2 ... A k A k+ 1 равна сумме углов k -угольника A 1 A 2 ... A k плюс сумма углов треугольника A 1 A k A k+ 1 . Но сумма углов k -угольника A 1 A 2 ... A k по предположению равна (k - 2)π, а сумма углов треугольника A 1 A k A k+ 1 равна π. Поэтому

S k+ 1 = S k + π = (k - 2)π + π = (k - 1)π.

Итак, оба условия принципа математической индукции выполняются, и потому формула (1) верна при любом натуральном п > 3.

Пример 2. Имеется лестница, все ступени которой одинаковы. Требуется указать минимальное число положений, которые гарантировали бы возможность «забраться» на любую по номеру ступеньку.

Все согласны с тем, что должно быть условие. Мы должны уметь забраться на первую ступень. Далее должны уметь с 1-ой ступеньки забраться на вторую. Потом во второй - на третью и т.д. на n-ую ступеньку. Конечно, в совокупности же «n» утверждений гарантирует нм то, что мы сможем добраться до n-ой ступеньки.

Посмотрим теперь на 2, 3,…., n положение и сравним их друг с другом. Легко заметить, что все они имеют одну и ту же структуру: если мы добрались до k ступеньки, то можем забраться на (k+1) ступеньку. Отсюда становится естественной такая аксиома для справедливости утверждений, зависящих от «n»: если предложение А(n), в котором n - натуральное число, выполняется при n=1 и из того, что оно выполняется при n=k (где k - любое натуральное число), следует, что оно выполняется и для n=k+1, то предположение А(n) выполняется для любого натурального числа n.

Приложение

Задачи с применением метода математической индукции при поступлении в ВУЗы.

Заметим, что при поступление в высшие учебные заведения также встречаются задачи, которые решаются данным методом. Рассмотрим их на конкретных примерах.

Пример 1. Доказать, что любом натуральном п справедливо равенство

1) При п=1 мы получаем верное равенство Sin.

2) Сделав предположение индукции, что при n=k равенство верно, рассмотрим сумму, стоящую в левой части равенства, при n=k+1;

3) Используя формулы приведения преобразуем выражение:

Тогда, в силу метода математической индукции равенство верно для любого натурального n.

Пример 2. Доказать, что для любого натурального n значение выражения 4n +15n-1 кратно 9.

1) При n=1: 2 2 +15-1=18 - кратно 9 (т.к.18:9=2)

2) Пусть равенство выполняется для n=k: 4 k +15k-1 кратно 9.

3) Докажем, что равенство выполняется и для следующего числа n=k+1

4 k+1 +15(k+1)-1=4 k+1 +15k+15-1=4.4 k +60k-4-45k+18=4(4 k +15k-1)-9(5k-2)

4(4 k +15k-1) - кратно 9;

9(5k-2) - кратно 9;

Следовательно и все выражение 4(4 k +15k-1)-9(5k-2) кратно 9, что и требовалось доказать.

Пример 3. Доказать, что при любом натуральном числе п выполняется условие: 1∙2∙3+2∙3∙4+…+ п(п+1)(п+2)=.

1) Проверим, что данная формула верна при п=1: Левая часть = 1∙2∙3=6.

Правая часть= . 6 = 6; верно при п=1.

2) Предположим, что данная формула верна при n=k:

1∙2∙3+2∙3∙4+…+k(k+1)(k+2)=. S k =.

3) Докажем, что данная формула верна при n=k+1:

1∙2∙3+2∙3∙4+…+(k+1)(k+2)(k+3)=.

S k+1 =.

Доказательство:

Итак, данное условие верно в двух случаях и доказали, что верно при n=k+1, следовательно она верно при любом натуральном числе п.

Заключение

Подведем итоги, в процессе исследования я выяснил, в чем заключается индукция, которая бывает полной или неполной, познакомился с методом математической индукции, основанном на принципе математической индукции, рассмотрел множество задач с применением данного метода.

Также я узнал много новой информации, отличной от той, что включена в школьную программу.Изучая метод математической индукции я использовал различную литературу, ресурсы интернета, а также консультировался с педагогом.

Вывод: Обобщив и систематизировав знания по математической индукции, убедился в необходимости знаний по данной теме в реальной действительности. Положительным качеством метода математической индукции является его широкое применение в решении задач: в области алгебры, геометрии и реальной математики. Также эти знания повышают интерес к математике, как к науке.

Я уверен, что навыки, приобретенные в ходе работы, помогут мне в будущем.

Список литературы

Соминский И.С. Метод математической индукции. Популярные лекции по математике, выпуск 3-М.: Наука, 1974г.

Л. И. Головина, И. М. Яглом. Индукция в геометрии. — Физматгиз, 1961. — Т. 21. — 100 с. — (Популярные лекции по математике).

Дорофеев Г.В., Потапов М.К., Розов Н.Х. Пособие по математике для поступающих в вузы (Избранные вопросы элементарной математики) - Изд.5-е, перераб., 1976 - 638с.

А. Шень. Математическая индукция. — МЦНМО, 2004. — 36 с.

M.Л.Галицкий, А.М.Гольдман, Л.И.Звавич Сборник задач по алгебре: учеб.пособие для 8-9 кл. с углубл. изучением математики 7-е изд.— М.: Просвещение, 2001.—271 с

Ма-ка-ры-чев Ю.Н., Мин-дюк Н.Г До-пол-ни-тель-ные главы к школь-но-му учеб-ни-ку ал-геб-ры 9 клас-са. - М.: Про-све-ще-ние, 2002.

Википедия- свободная энциклопедия.

Вступление

Основная часть

1. Полная и неполная индукция

2. Принцип математической индукции

3. Метод математической индукции

4. Решение примеров

5. Равенства

6. Деление чисел

7. Неравенства

Заключение

Список использованной литературы

Вступление

В основе всякого математического исследования лежат дедуктивный и индуктивный методы. Дедуктивный метод рассуждений - это рассуждение от общего к частному, т.е. рассуждение, исходным моментом которого является общий результат, а заключительным моментом – частный результат. Индукция применяется при переходе от частных результатов к общим, т.е. является методом, противоположным дедуктивному.

Метод математической индукции можно сравнить с прогрессом. Мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению развивать свою мысль логически, а значит, сама природа предначертала ему размышлять индуктивно.

Хотя и выросла область применения метода математической индукции, в школьной программе ему отводится мало времени. Ну, скажите, что полезного человеку принесут те два-три урока, за которые он услышит пять слов теории, решит пять примитивных задач, и, в результате получит пятёрку за то, что он ничего не знает.

А ведь это так важно - уметь размышлять индуктивно.

Основная часть

По своему первоначальному смыслу слово “индукция” применяется к рассуждениям, при помощи которых получают общие выводы, опираясь на ряд частных утверждений. Простейшим методом рассуждений такого рода является полная индукция. Вот пример подобного рассуждения.

Пусть требуется установить, что каждое натуральное чётное число n в пределах 4< n < 20 представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения:

4=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;

14=7+7; 16=11+5; 18=13+5; 20=13+7.

Эти девять равенств показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.

Таким образом, полная индукция заключается в том, что общее утверждение доказывается по отдельности в каждом из конечного числа возможных случаев.

Иногда общий результат удаётся предугадать после рассмотрения не всех, а достаточно большого числа частных случаев (так называемая неполная индукция).

Результат, полученный неполной индукцией, остается, однако, лишь гипотезой, пока он не доказан точным математическим рассуждением, охватывающим все частные случаи. Иными словами, неполная индукция в математике не считается законным методом строгого доказательства, но является мощным методом открытия новых истин.

Пусть, например, требуется найти сумму первых n последовательных нечётных чисел. Рассмотрим частные случаи:

1+3+5+7+9=25=5 2

После рассмотрения этих нескольких частных случаев напрашивается следующий общий вывод:

1+3+5+…+(2n-1)=n 2

т.е. сумма n первых последовательных нечётных чисел равна n 2

Разумеется, сделанное наблюдение ещё не может служить доказательством справедливости приведённой формулы.

Во многих случаях выход из такого рода затруднений заключается в обращении к особому методу рассуждений, называемому методом математической индукции. Он заключается в следующем.

Пусть нужно доказать справедливость некоторого утверждения для любого натурального числа n (например нужно доказать, что сумма первых n нечётных чисел равна n 2). Непосредственная проверка этого утверждения для каждого значения n невозможна, поскольку множество натуральных чисел бесконечно. Чтобы доказать это утверждение, проверяют сначала его справедливость для n=1. Затем доказывают, что при любом натуральном значении k из справедливости рассматриваемого утверждения при n=k вытекает его справедливость и при n=k+1.

Тогда утверждение считается доказанным для всех n. В самом деле, утверждение справедливо при n=1. Но тогда оно справедливо и для следующего числа n=1+1=2. Из справедливости утверждения для n=2 вытекает его справедливость для n=2+

1=3. Отсюда следует справедливость утверждения для n=4 и т.д. Ясно, что, в конце концов, мы дойдём до любого натурального числа n. Значит, утверждение верно для любого n.

Обобщая сказанное, сформулируем следующий общий принцип.

Принцип математической индукции.

Если предложение А(n ), зависящее от натурального числа n , истинно для n =1 и из того, что оно истинно для n=k (где k -любое натуральное число), следует, что оно истинно и для следующего числа n=k+1 , то предположение А(n ) истинно для любого натурального числа n .

В ряде случаев бывает нужно доказать справедливость некоторого утверждения не для всех натуральных чисел, а лишь для n>p, где p-фиксированное натуральное число. В этом случае принцип математической индукции формулируется следующим образом. Если предложение А(n ) истинно при n=p и если А(k ) Þ А(k+1) для любого k>p, то предложение А(n) истинно для любого n>p.

Доказательство по методу математической индукции проводиться следующим образом. Сначала доказываемое утверждение проверяется для n=1, т.е. устанавливается истинность высказывания А(1). Эту часть доказательства называют базисом индукции. Затем следует часть доказательства, называемая индукционным шагом. В этой части доказывают справедливость утверждения для n=k+1 в предположении справедливости утверждения для n=k (предположение индукции), т.е. доказывают, что А(k)ÞA(k+1).

ПРИМЕР 1

Доказать, что 1+3+5+…+(2n-1)=n 2 .

Решение: 1) Имеем n=1=1 2 . Следовательно,

утверждение верно при n=1, т.е. А(1) истинно.

2) Докажем, что А(k)ÞA(k+1).

Пусть k-любое натуральное число и пусть утверж-дение справедливо для n=k, т.е.

1+3+5+…+(2k-1)=k 2 .

Докажем, что тогда утверждение справедливо и для следующего натурального числа n=k+1, т.е. что

1+3+5+…+(2k+1)=(k+1) 2 .

В самом деле,

1+3+5+…+(2k-1)+(2k+1)=k 2 +2k+1=(k+1) 2 .

Итак, А(k)ÞА(k+1). На основании принципа математической индукции заключаем, что предпо-ложение А(n) истинно для любого nÎN.

ПРИМЕР 2

Доказать, что

1+х+х 2 +х 3 +…+х n =(х n+1 -1)/(х-1), где х¹1

Решение: 1) При n=1 получаем

1+х=(х 2 -1)/(х-1)=(х-1)(х+1)/(х-1)=х+1

следовательно, при n=1 формула верна; А(1) ис-тинно.

2) Пусть k-любое натуральное число и пусть формула верна при n=k, т.е.

1+х+х 2 +х 3 +…+х k =(х k+1 -1)/(х-1).

Докажем, что тогда выполняется равенство

1+х+х 2 +х 3 +…+х k +x k+1 =(x k+2 -1)/(х-1).

В самом деле

1+х+х 2 +x 3 +…+х k +x k+1 =(1+x+x 2 +x 3 +…+x k)+x k+1 =

=(x k+1 -1)/(x-1)+x k+1 =(x k+2 -1)/(x-1).

Итак, А(k)ÞA(k+1). На основании принципа математической индукции заключаем, что форму-ла верна для любого натурального числа n.

ПРИМЕР 3

Доказать, что число диагоналей выпуклого n-угольника равно n(n-3)/2.

Решение: 1) При n=3 утверждение спра-

А 3 ведливо, ибо в треугольнике

 А 3 =3(3-3)/2=0 диагоналей;

А 2 А(3) истинно.

2) Предположим, что во всяком

выпуклом k-угольнике имеет-

А 1 ся А k =k(k-3)/2 диагоналей.

А k Докажем, что тогда в выпуклом

(k+1)-угольнике число

диагоналей А k+1 =(k+1)(k-2)/2.

Пусть А 1 А 2 А 3 …A k A k+1 -выпуклый (k+1)-уголь-ник. Проведём в нём диагональ A 1 A k . Чтобы под-считать общее число диагоналей этого (k+1)-уголь-ника нужно подсчитать число диагоналей в k-угольнике A 1 A 2 …A k , прибавить к полученному числу k-2, т.е. число диагоналей (k+1)-угольника, исходящих из вершины А k+1 , и, кроме того, следует учесть диагональ А 1 А k .

Таким образом,

 k+1 = k +(k-2)+1=k(k-3)/2+k-1=(k+1)(k-2)/2.

Итак, А(k)ÞA(k+1). Вследствие принципа математической индукции утверждение верно для любого выпуклого n-угольника.

ПРИМЕР 4

Доказать, что при любом n справедливо утвер-ждение:

1 2 +2 2 +3 2 +…+n 2 =n(n+1)(2n+1)/6.

Решение: 1) Пусть n=1, тогда

Х 1 =1 2 =1(1+1)(2+1)/6=1.

Значит, при n=1 утверждение верно.

2) Предположим, что n=k

Х k =k 2 =k(k+1)(2k+1)/6.

3) Рассмотрим данное утвержде-ние при n=k+1

X k+1 =(k+1)(k+2)(2k+3)/6.

X k+1 =1 2 +2 2 +3 2 +…+k 2 +(k+1) 2 =k(k+1)(2k+1)/6+ +(k+1) 2 =(k(k+1)(2k+1)+6(k+1) 2)/6=(k+1)(k(2k+1)+

6(k+1))/6=(k+1)(2k 2 +7k+6)/6=(k+1)(2(k+3/2)(k+

2))/6=(k+1)(k+2)(2k+3)/6.

Мы доказали справедливость равенства и при n=k+1, следовательно, в силу метода математиче-ской индукции, утверждение верно для любого на-турального n.

ПРИМЕР 5

Доказать, что для любого натурального n спра-ведливо равенство:

1 3 +2 3 +3 3 +…+n 3 =n 2 (n+1) 2 /4.

Решение: 1) Пусть n=1.

Тогда Х 1 =1 3 =1 2 (1+1) 2 /4=1.

Мы видим, что при n=1 утверждение верно.

2) Предположим, что равенство верно при n=k

Лекция 6. Метод математической индукции.

Новые знания в науке и жизни добываются разными способами, но все они (если не углубляться в детали) делятся на два вида – переход от общего к частному и от частного к общему. Первый – это дедукция, второй – индукция. Дедуктивные рассуждения – это то, что в математике обычно называют логическими рассуждениями , и в математической науке дедукция является единственным законным методом исследования. Правила логических рассуждений были сформулированы два с половиной тысячелетия назад древнегреческим учёным Аристотелем. Он создал полный список простейших правильных рассуждений, силлогизмов – «кирпичиков» логики, одновременно указав типичные рассуждения, очень похожие на правильные, однако неправильные (с такими «псевдологическими» рассуждениями мы часто встречаемся в СМИ).

Индукция (induction – по-латыни наведение ) наглядно иллюстрируется известной легендой о том, как Исаак Ньютон сформулировал закон всемирного тяготения после того, как ему на голову упало яблоко. Ещё пример из физики: в таком явлении, как электромагнитная индукция, электрическое поле создает, «наводит» магнитное поле. «Ньютоново яблоко» – типичный пример ситуации, когда один или несколько частных случаев, то есть наблюдения , «наводят» на общее утверждение, общий вывод делается на основании частных случаев. Индуктивный метод является основным для получения общих закономерностей и в естественных, и в гуманитарных науках. Но он имеет весьма существенный недостаток: на основании частных примеров может быть сделан неверный вывод. Гипотезы, возникающие при частных наблюдениях, не всегда являются правильными. Рассмотрим пример, принадлежащий Эйлеру.

Будем вычислять значение трехчлена при некоторых первых значениях n :

Заметим, что получаемые в результате вычислений числа являются простыми. И непосредственно можно убедиться, что для каждого n от 1 до 39 значение многочлена
является простым числом. Однако при n =40 получаем число 1681=41 2 , которое не является простым. Таким образом, гипотеза, которая здесь могла возникнуть, то есть гипотеза о том, что при каждом n число
является простым, оказывается неверной.

Лейбниц в 17 веке доказал, что при всяком целом положительном n число
делится на 3, число
делится на 5 и т.д. На основании этого он предположил, что при всяком нечётном k и любом натуральном n число
делится на k , но скоро сам заметил, что
не делится на 9.

Рассмотренные примеры позволяют сделать важный вывод: утверждение может быть справедливым в целом ряде частных случаев и в то же время несправедливым вообще. Вопрос о справедливости утверждения в общем случае удается решить посредством применения особого метода рассуждений, называемого методом математической индукции (полной индукции, совершенной индукции).

6.1. Принцип математической индукции.

♦ В основе метода математической индукции лежит принцип математической индукции , заключающийся в следующем:

1) проверяется справедливость этого утверждения для n =1 (базис индукции) ,

2) предполагается справедливость этого утверждения для n = k , где k – произвольное натуральное число 1 (предположение индукции) , и с учётом этого предположения устанавливается справедливость его для n = k +1.

Доказательство . Предположим противное, то есть предположим, что утверждение справедливо не для всякого натурального n . Тогда существует такое натуральное m , что:

1) утверждение для n =m несправедливо,

2) для всякого n , меньшего m , утверждение справедливо (иными словами, m есть первое натуральное число, для которого утверждение несправедливо).

Очевидно, что m >1, т.к. для n =1 утверждение справедливо (условие 1). Следовательно,
– натуральное число. Выходит, что для натурального числа
утверждение справедливо, а для следующего натурального числа m оно несправедливо. Это противоречит условию 2. ■

Заметим, что в доказательстве использовалась аксиома о том, что в любой совокупности натуральных чисел содержится наименьшее число.

Доказательство, основанное на принципе математической индукции, называется методом полной математической индукции .

 Пример 6.1. Доказать, что при любом натуральном n число
делится на 3.

Решение.

1) При n =1 , поэтому a 1 делится на 3 и утверждение справедливо при n =1.

2) Предположим, что утверждение справедливо при n =k ,
, то есть что число
делится на 3, и установим, что при n =k +1 число делится на 3.

В самом деле,

Т.к. каждое слагаемое делится на 3, то их сумма также делится на 3. ■ 

 Пример 6.2. Доказать, что сумма первых n натуральных нечётных чисел равна квадрату их числа, то есть .

Решение. Воспользуемся методом полной математической индукции.

1) Проверяем справедливость данного утверждения при n =1: 1=1 2 – это верно.

2) Предположим, что сумма первых k (
) нечётных чисел равна квадрату числа этих чисел, то есть . Исходя из этого равенства, установим, что сумма первых k +1 нечётных чисел равна
, то есть .

Пользуемся нашим предположением и получаем

. ■ 

Метод полной математической индукции применяется для доказательства некоторых неравенств. Докажем неравенство Бернулли.

 Пример 6.3. Доказать, что при
и любом натуральном n справедливо неравенство
(неравенство Бернулли).

Решение. 1) При n =1 получаем
, что верно.

2) Предполагаем, что при n =k имеет место неравенство
(*). Используя это предположение, докажем, что
. Отметим, что при
это неравенство выполняется и поэтому достаточно рассмотреть случай
.

Умножим обе части неравенства (*) на число
и получим:

То есть (1+
. ■ 

Доказательство методом неполной математической индукции некоторого утверждения, зависящего от n , где
проводится аналогичным образом, но в начале устанавливается справедливость для наименьшего значения n .

В некоторых задачах явно не сформулировано утверждение, которое можно доказать методом математической индукции. В таких случаях надо самим установить закономерность и высказать гипотезу о справедливости этой закономерности, а затем методом математической индукции проверить предполагаемую гипотезу.

 Пример 6.4. Найти сумму
.

Решение. Найдём суммы S 1 , S 2 , S 3 . Имеем
,
,
. Высказываем гипотезу, что при любом натуральном n справедлива формула
. Для проверки этой гипотезы воспользуемся методом полной математической индукции.

1) При n =1 гипотеза верна, т.к.
.

2) Предположим, что гипотеза верна при n =k ,
, то есть
. Используя эту формулу, установим, что гипотеза верна и при n =k +1, то есть

В самом деле,

Итак, исходя из предположения, что гипотеза верна при n =k ,
, доказано, что она верна и при n =k +1, и на основании принципа математической индукции делаем вывод, что формула справедлива при любом натуральном n . ■ 

 Пример 6.5. В математике доказывается, что сумма двух равномерно непрерывных функций является равномерно непрерывной функцией. Опираясь на это утверждение, нужно доказать, что сумма любого числа
равномерно непрерывных функций является равномерно непрерывной функцией. Но поскольку мы ещё не ввели понятие «равномерно непрерывная функция», поставим задачу более абстрактно: пусть известно, что сумма двух функций, обладающих некоторым свойством S , сама обладает свойством S . Докажем, что сумма любого числа функций обладает свойством S .

Решение. Базис индукции здесь содержится в самой формулировке задачи. Сделав предположение индукции, рассмотрим
функций f 1 , f 2 , …, f n , f n +1 , обладающих свойством S . Тогда . В правой части первое слагаемое обладает свойством S по предположению индукции, второе слагаемое обладает свойством S по условию. Следовательно, их сумма обладает свойством S – для двух слагаемых «работает» базис индукции.

Тем самым утверждение доказано и будем использовать его далее. ■ 

 Пример 6.6. Найти все натуральные n , для которых справедливо неравенство

Решение. Рассмотрим n =1, 2, 3, 4, 5, 6. Имеем: 2 1 >1 2 , 2 2 =2 2 , 2 3 <3 2 , 2 4 =4 2 , 2 5 >5 2 , 2 6 >6 2 . Таким образом, можно высказать гипотезу: неравенство
имеет место для каждого
. Для доказательства истинности этой гипотезы воспользуемся принципом неполной математической индукции.

1) Как было установлено выше, данная гипотеза истинна при n =5.

2) Предположим, что она истинна для n =k ,
, то есть справедливо неравенство
. Используя это предположение, докажем, что справедливо неравенство
.

Т. к.
и при
имеет место неравенство

при
,

то получаем, что
. Итак, истинность гипотезы при n =k +1 следует из предположения, что она верна при n =k ,
.

Из пп. 1 и 2 на основании принципа неполной математической индукции следует, что неравенство
верно при каждом натуральном
. ■ 

 Пример 6.7. Доказать, что для любого натурального числа n справедлива формула дифференцирования
.

Решение. При n =1 данная формула имеет вид
, или 1=1, то есть она верна. Сделав предположение индукции, будем иметь:

что и требовалось доказать. ■ 

 Пример 6.8. Доказать, что множество, состоящее из n элементов, имеет подмножеств.

Решение. Множество, состоящее из одного элемента а , имеет два подмножества. Это верно, поскольку все его подмножества – пустое множество и само это множество, и 2 1 =2.

Предположим, что всякое множество из n элементов имеет подмножеств. Если множество А состоит из n +1 элементов, то фиксируем в нём один элемент – обозначим его d , и разобьём все подмножества на два класса – не содержащие d и содержащие d . Все подмножества из первого класса являются подмножествами множества В, получающегося из А выбрасыванием элемента d .

Множество В состоит из n элементов, и поэтому, по предположению индукции, у него подмножеств, так что в первом классе подмножеств.

Но во втором классе подмножеств столько же: каждое из них получается ровно из одного подмножества первого класса добавлением элемента d . Следовательно, всего у множества А
подмножеств.

Тем самым утверждение доказано. Отметим, что оно справедливо и для множества, состоящего из 0 элементов – пустого множества: оно имеет единственное подмножество – самого себя, и 2 0 =1. ■ 

МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ

Слово индукция по-русски означает наведение, а индуктивными называют выводы, на основе наблюдений, опытов, т.е. полученные путем заключения от частного к общему.

Например, мы каждый день наблюдаем, что Солнце восходит с востока. Поэтому можно быть уверенным, что и завтра оно появится на востоке, а не на западе. Этот вывод мы делаем, не прибегая ни к каким предположениям о причине движения Солнца по небу (более того, само это движение оказывается кажущимся, поскольку на самом деле движется земной шар). И, тем не менее, этот индуктивный вывод правильно описывает те наблюдения, которые мы проведем завтра.

Роль индуктивных выводов в экспериментальных науках очень велика. Они дают те положения, из которых потом путем дедукции делаются дальнейшие умозаключения. И хотя теоретическая механика основывается на трех законах движения Ньютона, сами эти законы явились результатом глубокого продумывания опытных данных, в частности законов Кеплера движения планет, выведенных им при обработке многолетних наблюдений датского астронома Тихо Браге. Наблюдение, индукция оказываются полезными и в дальнейшем для уточнения сделанных предположений. После опытов Майкельсона по измерению скорости света в движущейся среде оказалось необходимым уточнить законы физики, создать теорию относительности.

Лежащее в основе арифметики понятие следовать за тоже появилось при наблюдениях за строем солдат, кораблей и другими упорядоченными множествами.

Не следует, однако, думать, что этим исчерпывается роль индукции в математике. Разумеется, мы не должны экспериментально проверять теоремы, логически выведенные из аксиом: если при выводе не было сделано логических ошибок, то они постольку верны, поскольку истинны принятые нами аксиомы. Но из данной системы аксиом можно вывести очень много утверждений. И отбор тех утверждений, которые надо доказывать, вновь подсказывается индукцией. Именно она позволяет отделить полезные теоремы от бесполезных, указывает, какие теоремы могут оказаться верными, и даже помогает наметить путь доказательства.

Суть метода математической индукции

Во многих разделах арифметики, алгебры, геометрии, анализа приходится доказывать истинность предложений А(n), зависящих от натуральной переменной. Доказательство истинности предложения А(n) для всех значений переменной часто удается провести методом математической индукции, который основан на следующем принципе.

Предложение А(n) считается истинным для всех натуральных значений переменной, если выполнены следующие два условия:

Предложение А(n) истинно для n=1.

Из предположения, что А(n) истинно для n=k (где k - любое натуральное число), следует, что оно истинно и для следующего значения n=k+1.

Этот принцип называется принципом математической индукции. Обычно он выбирается в качестве одной из аксиом, определяющих натуральный ряд чисел, и, следовательно, принимается без доказательства.

Под методом математической индукции понимают следующий способ доказательства. Если требуется доказать истинность предложения А(n) для всех натуральных n, то, во-первых, следует проверить истинность высказывания А(1) и, во-вторых, предположив истинность высказывания А(k), попытаться доказать, что высказывание А(k+1) истинно. Если это удается доказать, причем доказательство остается справедливым для каждого натурального значения k, то в соответствии с принципом математической индукции предложение А(n) признается истинным для всех значений n.

Метод математической индукции широко применяется при доказательстве теорем, тождеств, неравенств, при решении задач на делимость, при решении некоторых геометрических и многих других задач.

Метод математической индукции в решении задач на

делимость

С помощью метода математической индукции можно доказывать различные утверждения, касающиеся делимости натуральных чисел.

Следующее утверждение можно сравнительно просто доказать. Покажем, как оно получается с помощью метода математической индукции.

Пример 1 . Если n - натуральное число, то число четное.

При n=1 наше утверждение истинно: - четное число. Предположим, что - четное число. Так как , a 2k - четное число, то и четное. Итак, четность доказана при n=1, из четности выведена четность .Значит, четно при всех натуральных значениях n.

Пример 2. Доказать истинность предложения

A(n)={число 5 кратно 19}, n - натуральное число.

Решение.

Высказывание А(1)={число кратно 19} истинно.

Предположим, что для некоторого значения n=k

А(k)={число кратно 19} истинно. Тогда, так как

Очевидно, что и A(k+1) истинно. Действительно, первое слагаемое делится на 19 в силу предположения, что A(k) истинно; второе слагаемое тоже делится на 19, потому что содержит множитель 19. Оба условия принципа математической индукции выполнены, следовательно, предложение A(n) истинно при всех значениях n.

Применение метода математической индукции к

суммированию рядов

Пример 1. Доказать формулу

, n - натуральное число.

Решение.

При n=1 обе части равенства обращаются в единицу и, следовательно, первое условие принципа математической индукции выполнено.

Предположим, что формула верна при n=k, т.е.

Прибавим к обеим частям этого равенства и преобразуем правую часть. Тогда получим

Таким образом, из того, что формула верна при n=k, следует, что она верна и при n=k+1. Это утверждение справедливо при любом натуральном значении k. Итак, второе условие принципа математической индукции тоже выполнено. Формула доказана.

Пример 2. Доказать, что сумма n первых чисел натурального ряда равна .

Решение.

Обозначим искомую сумму , т.е. .

При n=1 гипотеза верна.

Пусть . Покажем, что .

В самом деле,

Задача решена.

Пример 3. Доказать, что сумма квадратов n первых чисел натурального ряда равна .

Решение.

Пусть .

Предположим, что . Тогда

И окончательно .

Пример 4. Доказать, что .

Решение.

Если , то

Пример 5. Доказать, что

Решение.

При n=1 гипотеза очевидно верна.

Пусть .

Докажем, что .

Действительно,

Примеры применения метода математической индукции к

доказательству неравенств

Пример 1. Доказать, что при любом натуральном n>1

Решение.

Обозначим левую часть неравенства через .

Следовательно, при n=2 неравенство справедливо.

Пусть при некотором k. Докажем, что тогда и . Имеем , .

Сравнивая и , имеем , т.е. .

При любом натуральном k правая часть последнего равенства положительна. Поэтому . Но , значит, и .

Пример 2. Найти ошибку в рассуждении.

Утверждение. При любом натуральном n справедливо неравенство .

Доказательство.

. (1)

Докажем, что тогда неравенство справедливо и при n=k+1, т.е.

Действительно, не меньше 2 при любом натуральном k. Прибавим к левой части неравенства (1) , а к правой 2. Получим справедливое неравенство , или . Утверждение доказано.

Пример 3. Доказать, что , где >-1, , n - натуральное число, большее 1.

Решение.

При n=2 неравенство справедливо, так как .

Пусть неравенство справедливо при n=k, где k - некоторое натуральное число, т.е.

. (1)

Покажем, что тогда неравенство справедливо и при n=k+1, т.е.

. (2)

Действительно, по условию, , поэтому справедливо неравенство

, (3)

полученное из неравенства (1) умножением каждой части его на . Перепишем неравенство (3) так: . Отбросив в правой части последнего неравенства положительное слагаемое , получим справедливое неравенство (2).

Пример 4. Доказать, что

(1)

где , , n - натуральное число, большее 1.

Решение.

При n=2 неравенство (1) принимает вид

. (2)

Так как , то справедливо неравенство

. (3)

Прибавив к каждой части неравенства (3) по , получим неравенство (2).

Этим доказано, что при n=2 неравенство (1) справедливо.

Пусть неравенство (1) справедливо при n=k, где k - некоторое натуральное число, т.е.

. (4)

Докажем, что тогда неравенство (1) должно быть справедливо и при n=k+1, т.е.

(5)

Умножим обе части неравенства (4) на a+b. Так как, по условию, , то получаем следующее справедливое неравенство:

. (6)

Для того чтобы доказать справедливость неравенства (5), достаточно показать, что

, (7)

или, что то же самое,

. (8)

Неравенство (8) равносильно неравенству

. (9)

Если , то , и в левой части неравенства (9) имеем произведение двух положительных чисел. Если , то , и в левой части неравенства (9) имеем произведение двух отрицательных чисел. В обоих случаях неравенство (9) справедливо.

Этим доказано, что из справедливости неравенства (1) при n=k следует его справедливость при n=k+1.

Метод математической индукции в применение к другим

задачам

Наиболее естественное применение метода математической индукции в геометрии, близкое к использованию этого метода в теории чисел и в алгебре, - это применение к решению геометрических задач на вычисление. Рассмотрим несколько примеров.

Пример 1. Вычислить сторону правильного - угольника, вписанного в круг радиуса R.

Решение.

При n=2 правильный 2 n - угольник есть квадрат; его сторона . Далее, согласно формуле удвоения

находим, что сторона правильного восьмиугольника , сторона правильного шестнадцатиугольника , сторона правильного тридцатидвухугольника . Можно предположить поэтому, что сторона правильного вписанного 2 n - угольника при любом равна

. (1)

Допустим, что сторона правильного вписанного - угольника выражается формулой (1). В таком случае по формуле удвоения

откуда следует, что формула (1) справедлива при всех n.

Пример 2. На сколько треугольников n-угольник (не обязательно выпуклый) может быть разбит своими непересекающимися диагоналями?

Решение.

Для треугольника это число равно единице (в треугольнике нельзя провести ни одной диагонали); для четырехугольника это число равно, очевидно, двум.

Предположим, что мы уже знаем, что каждый k-угольник, где k 1 А 2 …А n на треугольники.

А n

А 1 А 2

Пусть А 1 А k - одна из диагоналей этого разбиения; она делит n-угольник А 1 А 2 …А n на k-угольник A 1 A 2 …A k и (n-k+2)-угольник А 1 А k A k+1 …A n . В силу сделанного предположения, общее число треугольников разбиения будет равно

(k-2)+[(n-k+2)-2]=n-2;

тем самым наше утверждение доказано для всех n.

Пример 3. Указать правило вычисления числа P(n) способов, которыми выпуклый n-угольник может быть разбит на треугольники непересекающимися диагоналями.

Решение.

Для треугольника это число равно, очевидно, единице: P(3)=1.

Предположим, что мы уже определили числа P(k) для всех k 1 А 2 …А n . При всяком разбиении его на треугольники сторона А 1 А 2 будет стороной одного из треугольников разбиения, третья вершина этого треугольника может совпасть с каждой из точек А 3 , А 4 , …,А n . Число способов разбиения n-угольника, при которых эта вершина совпадает с точкой А 3 , равно числу способов разбиения на треугольники (n-1)-угольника А 1 А 3 А 4 …А n , т.е. равно P(n-1). Число способов разбиения, при которых эта вершина совпадает с А 4 , равно числу способов разбиения (n-2)-угольника А 1 А 4 А 5 …А n , т.е. равно P(n-2)=P(n-2)P(3); число способов разбиения, при которых она совпадает с А 5 , равно P(n-3)P(4), так как каждое из разбиений (n-3)-угольника А 1 А 5 …А n можно комбинировать при этом с каждым из разбиений четырехугольника А 2 А 3 А 4 А 5 , и т.д. Таким образом, мы приходим к следующему соотношению:

Р(n)=P(n-1)+P(n-2)P(3)+P(n-3)P(4)+…+P(3)P(n-2)+P(n-1).

С помощью этой формулы последовательно получаем:

P(4)=P(3)+P(3)=2,

P(5)=P(4)+P(3)P(3)+P(4)+5,

P(6)=P(5)+P(4)P(3)+P(3)P(4)+P(5)=14

и т.д.

Так же при помощи метода математической индукции можно решать задачи с графами.

Пусть на плоскости задана сеть линий, соединяющих между собой какие-то точки и не имеющие других точек. Такую сеть линий мы будем называть картой, заданные точки ее вершинами, отрезки кривых между двумя смежными вершинами - границами карты, части плоскости, на которые она разбивается границами - странами карты.

Пусть на плоскости задана некоторая карта. Мы будем говорить, что она правильно раскрашена, если каждая ее страна закрашена определенной краской, причем любые две страны, имеющие между собой общую границу, закрашены в разные цвета.

Пример 4. На плоскости дано n окружностей. Доказать, что при любом расположении этих окружностей образуемую ими карту можно правильно раскрасить двумя красками.

Решение.

При n=1 наше утверждение очевидно.

Предположим, что наше утверждение справедливо для любой карты, образованной n окружностями, и пусть на плоскости задано n+1 окружностей. Удалив одну из этих окружностей, мы получим карту, которую в силу сделанного предположения можно правильно раскрасить двумя красками, например черной и белой.

Во многих разделах математики приходится доказывать истинность утверждения, зависящего от , т.е. истинность высказывания p(n) для "n ÎN (для любого n ÎN p(n) верно).

Часто это удается доказать методом математической индукции.

В основе этого метода лежит принцип математической индукции. Обычно он выбирается в качестве одной из аксиом арифметики и, следовательно, принимается без доказательства. Согласно принципу математической индукции предложение p(n) считается истинным для всех натуральных значений переменной, если выполнены два условия:

1. Предложение p(n) истинно для n = 1.

2. Из предложения, что p(n) истинно для n = k (k — произвольное натуральное число) следует, что оно истинно для n = k + 1.

Под методом математической индукции понимают следующий способ доказательства

1. Проверяют истинность утверждения для n = 1 – база индукции.

2. Предполагают, что утверждение верно для n = k – индуктивное предположение.

3. Доказывают, что тогда оно верно и для n = k + 1 индуктивный переход.

Иногда предложение p(n) оказывается верным не для всех натуральных n , а начиная с некоторого для n = n 0. В этом случае в базе индукции проверяется истинность p(n) при n = n 0.

Пример 1. Пусть . Доказать, что

1. База индукции: при n = 1 по определению S 1 = 1 и по формуле получаем один результат. Утверждение верно.

n = k и .

n = k + 1. Докажем, что .

Действительно, в силу индуктивного предположения

Преобразуем это выражение

Индуктивный переход доказан.

Замечание. Полезно записать, что дано (индуктивное предположение) и что нужно доказать!

Пример 2. Доказать

1. База индукции. При n = 1, утверждение, очевидно, верно.

2. Индуктивное предположение. Пусть n = k и

3. Индуктивный переход. Пусть n = k + 1. Докажем:

Действительно, возведем правую сторону в квадрат как сумму двух чисел:

Используя индуктивное предположение и формулу суммы арифметической прогрессии: , получим

Пример 3. Доказать неравенство

1. Базой индукции в этом случае является проверка истинности утверждения для , т.е. необходимо проверить неравенство . Для этого достаточно возвести неравенство в квадрат: или 63 < 64 – неравенство верно.

2. Пусть неравенство верно для , т.е.

3. Пусть , докажем:

Используем предположение индукции

Зная как должна выглядеть правая сторона в доказываемом неравенстве выделим эту часть

Остается установить, что лишний множитель не превосходит единицы. Действительно,

Пример 4. Доказать, что при любом натуральном число оканчивается цифрой .

1. Наименьшее натуральное , с которого справедливо утверждение, равно . .

2. Пусть при число оканчивается на . Это означает, что это число можно записать в виде , где – какое-то натуральное число. Тогда .

3. Пусть . Докажем, что оканчивается на . Используя полученное представление, получим

Последнее число имеет ровно единиц.

Приложение

1.4. Метод математической индукции

Как известно, математические утверждения (теоремы) должны быть обоснованы, доказаны. Мы сейчас познакомимся с одним из методов доказательства - методом математической индукции.

В широком смысле индукция - это способ рассуждений, позволяющий переходить от частных утверждений к общим. Обратный переход, от общих утверждений к частным, называется дедукцией.

Дедукция всегда приводит к правильным выводам. Например, нам известен общий результат: все целые числа, оканчивающиеся на нуль, делятся на 5. Отсюда, конечно, можно сделать вывод, что и любое конкретное число, оканчивающееся на 0, например 180, делится на 5.

В то же время индукция может привести к неверным выводам. Например, замечая, что число 60 делится на числа 1, 2, 3, 4, 5, 6, мы не вправе сделать вывод о том, что 60 делится вообще на любое число.

Метод математической индукции позволяет во многих случаях строго доказывать справедливость общего утверждения P(n), в формулировку которого входит натуральное число n.

Применение метода включает 3 этапа.

1) База индукции: проверяем справедливость утверждения P(n) для n = 1 (или для другого, частного значения n, начиная с которого предполагается справедливость P(n)).

2) Предположение индукции: предполагаем, что P(n) справедливо при n = k.

3) Шаг индукции: используя предположение, доказываем, что P(n) справедливо для n = k + 1.

В результате можно сделать вывод о справедливости P(n) для любого n ∈ N. Действительно, для n = 1 утверждение верно (база индукции). А следовательно, верно и для n = 2, так как переход от n = 1 к n = 2 обоснован (шаг индукции). Применяя шаг индукции снова и снова, получаем справедливость P(n) для n = 3, 4, 5, . . ., т. е. справедливость P(n) для всех n.

Пример 14. Сумма первых n нечётных натуральных чисел равна n2: 1 + 3 + 5 + …

+ (2n — 1) = n2.

Доказательство проведём методом математической индукции.

1) База: при n=1 слева только одно слагаемое, получаем: 1 = 1.

Утверждение верно.

2) Предположение: предполагаем, что для некоторого k справедливо равенство: 1 + 3 + 5 + … + (2k — 1) = k2.

Решение задач про вероятность попаданий при выстрелах

Общая постановка задачи следующая:

Вероятность попадания в цель при одном выстреле равна $p$. Производится $n$ выстрелов. Найти вероятность того, что цель будет поражена в точности $k$ раз (будет $k$ попаданий).

Применяем формулу Бернулли и получаем:

$$ P_n(k)=C_n^k \cdot p^k \cdot (1-p)^{n-k} = C_n^k \cdot p^k \cdot q^{n-k}.

Здесь $C_n^k$ — число сочетаний из $n$ по $k$.

Если в задаче речь идет о нескольких стрелках с разными вероятностями попадания в цель, теорию, примеры решения и калькулятор вы можете найти здесь.

Видеоурок и шаблон Excel

Посмотрите наш ролик о решении задач о выстрелах в схеме Бернулли, узнайте, как использовать Excel для решения типовых задач.

Расчетный файл Эксель из видео можно бесплатно скачать и использовать для решения своих задач.

Примеры решений задач о попаданиях в цель в серии выстрелов

Рассмотрим несколько типовых примеров.

Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,705. Найти вероятность того, что при этом будет ровно 5 попаданий.

Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах по мишени), всего производится $n=7$ выстрелов, вероятность попадания при каждом $p=0,705$, вероятность промаха $q=1-p=1-0,705=0,295$.

Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем: $$ P_7(5)=C_{7}^5 \cdot 0,705^5 \cdot 0,295^2 = 21\cdot 0,705^5 \cdot 0,295^2= 0,318. $$

Пример 2. Вероятность попадания в мишень при одном выстреле равна 0,4.

По мишени производится четыре независимых выстрела. Найти вероятность того, что будет хотя бы одно попадание в мишень.

Изучаем задачу и выписываем параметры: $n=4$ (выстрела), $p=0,4$ (вероятность попадания), $k \ge 1$ (будет хотя бы одно попадание).

Используем формулу для вероятности противоположного события (нет ни одного попадания):

$$ P_4(k \ge 1) = 1-P_4(k \lt 1) = 1-P_4(0)= $$ $$ =1-C_{4}^0 \cdot 0,4^0 \cdot 0,6^4 =1- 0,6^4=1- 0,13=0,87. $$

Вероятность попасть хотя бы один раз из четырех равна 0,87 или 87%.

Пример 3. Вероятность поражения мишени стрелком равна 0,3.

Найти вероятность того, что при 6 выстрелах мишень будет поражена от трех до шести раз.

В отличие от предыдущих задач, здесь нужно найти вероятность того, что число попаданий будет находится в некотором интервале (а не равно в точности какому-то числу). Но формула используется прежняя.

Найдем вероятность того, что мишень будет поражена от трех до шести раз, то есть будет или 3, или 4, или 5, или 6 попаданий.

Данные вероятности вычислим по формуле (1):

$$ P_6(3)=C_{6}^3 \cdot 0,3^3\cdot 0,7^3 = 0,185. $$ $$ P_6(4)=C_{6}^4 \cdot 0,3^4\cdot 0,7^2 = 0,06. $$ $$ P_6(5)=C_{6}^5 \cdot 0,3^5\cdot 0,7^1 = 0,01. $$ $$ P_6(6)=C_{6}^6 \cdot 0,3^6\cdot 0,7^0 = 0,001.

Так как события несовместные, искомая вероятность может быть найдена по формуле сложения вероятностей: $$ P_6(3 \le k \le 6)=P_6(3)+P_6(4)+P_6(5)+P_6(6)=$$ $$ = 0,185+0,06+0,01+0,001=0,256.$$

Пример 4. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

Обозначим вероятность попадания в цель при одном выстреле. Введем событие:
$A = $ (Из четырех выстрелов хотя бы один попадет в цель),
а также противоположное ему событие, которое можно записать как:
$\overline{A} = $ (Все 4 выстрела будут мимо цели, ни одного попадания).

Запишем формулу для вероятности события $A$.

Выпишем известные значения: $n=4$, $P(A)=0,9984$. Подставляем в формулу (1) и получаем:

$$ P(A)=1-P(\overline{A})=1-P_4(0)=1-C_{4}^0 \cdot p^0 \cdot (1-p)^4=1-(1-p)^4=0,9984.

Решаем получившееся уравнение:

$$ 1-(1-p)^4=0,9984,\\ (1-p)^4=0,0016,\\ 1-p=0,2,\\ p=0,8. $$

Итак, вероятность попадания в цель при одном выстреле равна 0,8.

Спасибо, что читаете и делитесь с другими

Полезные ссылки

Найдите готовые задачи в решебнике:

Онлайн-расчеты по формуле Бернулли

Решение неравенства с помощью калькулятора

Неравенство в математике относится ко всем уравнениям, где «=» заменяется любым из следующих значков: \ [> \] \ [\ geq \] \ [

* линейный;

* квадратный;

* дробный;

* индикативный;

* тригонометрический;

* логарифмический.

В зависимости от этого неравенства называются линейными, частичными и т. Д.

Вы должны знать об этих признаках:

* неравенства с значком больше (>) или меньше (

* Неравенства с значками, которые больше или равны \ [\ geq \] меньше или равно [\ leq \], называются непрофессиональными;

* значок не тот же \ [\ ne \] один, но необходимо постоянно разрешать случаи с этим значком.

Такое неравенство решается посредством преобразований тождеств.

Также прочитайте нашу статью «Решите полное решение для онлайн-уравнения»

Предположим, что выполнено неравенство следующего:

Мы решаем его так же, как линейное уравнение, но следует внимательно следить за признаком неравенства.

Сначала мы переносим членов из неизвестного влево, от известного до правого, меняя символы на противоположное:

Затем мы разделим обе стороны на -4 и изменим знак неравенства на противоположное:

Это ответ на это уравнение.

Где я могу решить неравенство в Интернете?

Вы можете решить уравнение на нашем сайте pocketteacher.ru.

Калькулятор неравенства Бернулли

В считанные секунды бесплатное онлайн-решение для спасения решит онлайн-уравнение любой сложности. Все, что вам нужно сделать, это ввести ваши данные в спасение. Вы также можете просмотреть видео-инструкции и узнать, как решить уравнение на нашем веб-сайте.

И если у вас есть вопросы, вы можете задать их в нашей группе Vkontakte: pocketteacher. Присоединяйтесь к нашей группе, мы будем рады вам помочь.