Проецирование три взаимно перпендикулярные плоскости. Open Library - открытая библиотека учебной информации
Система трех взаимно перпендикулярных плоскостей
Образование комплексного чертежа (эпюра)
Для удобства пользования полученными изображениями от пространственной системы плоскостей перейдем к плоскостной.
Для этого:
1. Применим способ вращения плоскости p 1 вокруг оси Х до совмещения с плоскостью p 2 (рис. 1)
2. Совмещаем плоскости p 1 и p 2 в одну плоскость чертежа (рис. 2)
| Рисунок 1 | Рисунок 2 |
Проекции А 1 и А 2 располагаются на одной линии связи перпендикулярной оси Х. Эта линия принято называть линией проекционной связи (рис. 3).
Рисунок 3
Так как плоскость проекций считается бесконечной в пространстве, то границы плоскости p 1 , p 2 можно не изображать (рис. 4).
Рисунок 4
В результате совмещения плоскостей p 1 и p 2 получается комплексный чертеж или эпюр (от франц. epure чертеж), ᴛ.ᴇ. чертеж в системе p 1 и p 2 или в системе двух плоскостей проекций. Заменив наглядное изображение эпюром, мы утратили пространственную картину расположения плоскостей проекций и точки. Но эпюр обеспечивает точность и удобоизмеряемость изображений при значительной простоте построений.
Точка, заданная в пространстве, может иметь различные положения относительно плоскостей проекций.
Построение изображений точки может быть осуществлено различными способами:
- словами (вербальное);
- графически (чертежи);
- наглядное изображение (объемное);
- плоскостное (комплексный чертеж).
Таблица 1
Пример изображения точек, принадлежащих плоскостям p 1 и p 2
| Положение точки | Наглядное изображение | Комплексный чертеж | Характерные признаки |
| Точка А принадлежит плоскости p 1 | А 1 – ниже оси Х, А 2 – на оси X | ||
| Точка B принадлежит плоскости p 1 | B 1 – выше оси X, B 2 – на оси X | ||
| Точка С принадлежит плоскости p 2 | С 2 – выше оси X, С 1 – на оси Х | ||
| Точка D принадлежит плоскости p 2 | D 1 – на оси X, D 2 – ниже оси X | ||
| Точка Е принадлежит оси X | E 1 совпадает с E 2 и принадлежит оси X |
Рисунок 1
Рассмотрим три взаимно перпендикулярные плоскости p 1 , p 2 , p 3 (рис. 1). Вертикальная плоскостьp 3 называется профильной плоскостью проекции. Пересекаясь между собой, плоскостиp 1 , p 2 , p 3 образуют оси проекций, при этом пространство делится на 8 октантов.
p 1 p 2 = x; -x
p 1 p 3 = у; -у
p 2 p 3 = z; -z
0 – точка пересечения осей проекций.
Плоскости проекций, попарно пересекаясь, определяют три оси x, y, z, которые можно рассматривать как систему декартовых координат: ось Х принято называть осью абцисс, ось y – осью ординат, ось Z – осью аппликат, точка пересечения осей, обозначаемая буквой О, есть начало координат.
Для получения комплексного чертежа применим способ вращения плоскостей p 1 и p 3 до совмещения с плоскостью p 2 . Окончательный вид всех плоскостей в первом октанте приведен на рис. 2.
Рисунок 2
Здесь оси Оx и Оz , лежащие в неподвижной плоскости p 2 , изображены только один раз, ось Оy показана дважды. Объясняется это тем, что, вращаясь с плоскостью p 1 , ось y на эпюре совмещается с осью Оz , а вращаясь с плоскостью p 3 , эта же ось совмещается с осью Оx .
Любая точка пространства задается координатами. По знакам координат можно определить октант, в котором находится заданная точка. Для этого воспользуемся табл. 1, в которой рассмотрены знаки координат в 1–4 октантах (5–8 октанты не представлены, они имеют отрицательное значение х , а y и z повторяются).
Таблица 1
| x | y | z | Октант |
| + | + | + | I |
| + | _ | + | II |
| + | _ | _ | III |
| + | + | _ | IV |
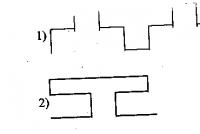
Существует множество деталей, информацию о форме которых невозможно передать двумя проекциями чертежа (рис. 75).
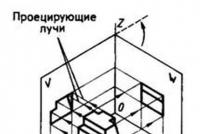
Для того чтобы информация о сложной форме детали была представлена достаточно полно, используют проецирование на три взаимно перпендикулярные плоскости проекции: фронтальную - V, горизонтальную - H и профильную - W (читается «дубль вэ»).
Система плоскостей проекций представляет собой трехгранный угол с вершиной в точке О. Пересечения плоскостей трехгранного угла образуют прямые линии - оси проекций (OX, OY, OZ) (рис. 76).
В трехгранный угол помещают предмет так, чтобы его формообразующая грань и основание были бы параллельны соответственно фронтальной и горизонтальной плоскостям проекций. Затем через все точки предмета проводят проецирующие лучи, перпендикулярные всем трем плоскостям проекций, на которых получают фронтальную, горизонтальную и профильную проекции предмета. После проецирования предмет удаляют из трехгранного угла, а затем горизонтальную и профильную плоскости проекций поворачивают на 90* соответственно вокруг осей ОХ и OZ до совмещения с фронтальной плоскостью проекции и получают чертеж детали, содержащий три проекции.
Рис. 75. Проецирование на две плоскости проекций не всегда дает
полное представление о форме предмета


Рис. 76. Проецирование на три взаимно перпендикулярные
плоскости проекций
Три проекции чертежа взаимосвязаны друг с другом. Фронтальная и горизонтальная проекции сохраняют проекционную связь изображений, т. е. устанавливаются проекционные связи и между фронтальной и горизонтальной, фронтальной и профильной, а также горизонтальной и профильной проекциями (см. рис. 76). Линии проекционной связи определяют местоположение каждой проекции на поле чертежа.
Во миогнх странах мира принята другая система прямо- угольного проецирования на три взаимно перпендикулярные плоскости проекций, которая условно называется «американская» (см. Приложение 3). Основное eе отличие состоит в том, что по-иному, относительно проецируемого объекта, в пространстве располагается трехгранный угол и в других направлениях разворачиваются плоскости проекций. Поэтому горизонтальная проекция оказывается над фронтальной, а профильная проекция - справа от фронтальной.
Форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как изображаются геометрические тела в системе трех проекций на производстве (табл. 7). (Чертежи, содержащие три проекции, называются комплексными чертежами.)
7. Комплексные и производственные чертежи деталей простой геометрической формы



П p и м e ч а н и я: 1. В зависимости от особенностей производственного процесса на чертеже изображают определенное число проекций. 2. На чертежах принято давать наименьшее, но достаточное число изображений для определения формы предмета. Число изображений чертежа можно уменьшить, используя условные знаки s, l, ? которых вы уже знаете.
При решении задач бывает недостаточно двух проекций. Поэтому вводят третью плоскость перпендикулярно плоскостям П 1 и П 2 . Ее называют профильной плоскостью (П 3 ) .
Три плоскости делят пространство на 8 частей – октантов (рис. 6). Как и прежде, будем считать, что зритель, рассматривающий предмет, находится в первом октанте. Чтобы получить эпюр (рис. 7) любого геометрического образа плоскости П 1 и П 3 вращают, как показано на рис. 6.
Плоскости проекций, попарно пересекаясь, определяют три оси x , y и z , которые можно рассматривать как систему декартовых координат в пространстве с началом в точке О .
Для получения эпюра точки в системе трех плоскостей проекций плоскости П 1 и П 3 вращают до совмещения с плоскостью П 2 (рис. 8). При обозначении осей на эпюре отрицательные полуоси обычно не указывают.
Для нахождения профильной проекции точки поступают следующим образом: из фронтальной проекции А 2 точки А проводят прямую перпендикулярно оси Z и на этой прямой от оси z откладывают отрезок, равный координате у точки А (рис. 9).

Рис.8 Рис. 9
Координатами называют числа, которые ставят в соответствие точке для определения ее положения в пространстве или на поверхности. В трехмерном пространстве положение точки устанавливают с помощью прямоугольных декартовых координат x
, y
и z
(абсцисса, ордината и аппликата):
а
?
бсцисса
х
= ………..= …..…..= ….….. = ……….. – расстояние от точки до плоскости П 3;
ордината у = ……….= ………= …...... = ………… – расстояние от точки до плоскости П 2;
аппликата
z= …….. = ………= ……..= ………… – расстояние от точки до плоскости П 1
А
1
А
2
– вертикальная линия связи, перпендикулярная оси х;
А
2
А
3
– горизонтальная линия связи, перпендикулярная оси
z
.
А
?
1
(….,….) Положение проекции каждой точки
А 2 (….,….) определяется двумя координатами
А
3
(….,….)
Если точка принадлежит хотя бы одной плоскости проекций, она занимает частное
положение относительно плоскостей проекций. Если точка не принадлежит ни одной из плоскостей проекций, она занимает общее
положение.
Лекция № 2
ПРЯМАЯ
1. Прямая. 2. Положение прямой относительно плоскостей проекций. 3. Принадлежность точки прямой. 4. Следы прямой. 5. Деление отрезка прямой в данном соотношении. 6. Определение длины отрезка прямой и углов наклона прямой к плоскостям проекций. 7. Взаимное положение прямых.
1 ПРЯМАЯ
ПРЯМАЯ
Проекцией прямой в общем случае является прямая, за исключением случая, когда прямая перпендикулярна плоскости (рис. 10).
Чтобы построить эпюр прямой определяют координаты x , y , z двух точек прямой и переносят эти величины на чертеж.
2 ПОЛОЖЕНИЕ ПРЯМОЙ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИИ
В
зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
П роекция прямой общего положения меньше самой прямой.
роекция прямой общего положения меньше самой прямой.
Различают восходящую прямую – это прямая, которая по мере удаления от наблюдателя повышается (рис. 11) и нисходящую, которая понижается.

h П 1 ; Z = const
h 2 0x признак
h 3 0у горизонтали
h 1 = h – свойство
горизонтали
– угол наклона прямой к
плоскости П 1
– угол наклона прямой к
плоскости П 2
– угол наклона прямой к
плоскости П 3
?
= 0
= (h 1 П 2) обозначить
Рис. 12. Горизонталь
= (h
1 П 3) на чертеже

f П 2 ; у = const
f 1 0x признак
f 3 0z фронтали
f
2 = f
– свойство фронтали
?
= 0
= (f 2 П 1) обозначить
= (f 2 П 3) на чертеже
Рис. 13. Фронталь
р П 3 ; х = const
р
 1 0у
признак
1 0у
признак
р 2 0z профильной прямой
р 3 = р – свойство профильной
прямой
= 0
?
= (р
3 П 1) обозначить
= (р 3 П 2) на чертеже
Рис. 14. Профильная прямая

а П 1
а 2 0х признак
а
3 0у
?
=

b
П 2
b 1 0х признак
b
3 0z
?
=

c П 3
c 1 0у признак
с
2 0z
?
=
3 ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПРЯМОЙ
Т еорема:
Если в пространстве точка принадлежит прямой, то на эпюре проекции этой точки находятся на одноименных проекциях прямой (рис. 18):
еорема:
Если в пространстве точка принадлежит прямой, то на эпюре проекции этой точки находятся на одноименных проекциях прямой (рис. 18):
М АВ ,
Е
АВ
.
Справедлива обратная теорема
:
М 1 A 1 B 1 ;
М 2 A 2 B 2 М АВ .
4 СЛЕДЫ ПРЯМОЙ
С
?
лед
– это точка пересеченная прямой с плоскостью проекций
(рис. 19).
Так как след принадлежит одной из плоскостей проекций, то его одна координата должна быть равна нулю.
обозначить на H = k ∩ П 1 – горизонтальный след
чертеже (рис. 19) F = k ∩ П 2 – фронтальный след
?
Р =
k
∩
П 3
– профильный след
Правило построения следов:
Для построения горизонтального следа прямой ….. необходимо фронтальную проекцию ….. прямой ….. продолжить до пересечения с осью Х , затем из точки пересечения с осью Х восстановить к ней перпендикуляр, и продолжить горизонтальную ….. проекцию прямой …… до пересечения с этим перпендикуляром.
Фронтальный след строиться аналогично.
5 ДЕЛЕНИЕ ОТРЕЗКА ПРЯМОЙ В ДАННОМ СООТНОШЕНИИ
Из свойств параллельного проецирования известно , что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же соотношении.
Поэтому, чтобы некоторый отрезок разделить на эпюре в данном соотношении, надо в том же отношении разделить его проекции.
Зная это условие можно определить принадлежность точки К прямой АВ : А 2 К 2 : К 2 В 2 ¹ А 1 К 1 : К 1 В 1 Þ К Ï АВ
Пример: Чтобы разделить отрезок АВ в отношении 2: 3 из точки А 1 проведем произвольный отрезок А 1 В 0 1 разделенный на пять равных частей (рис. 20): A 1 K 0 1 = 2 частям, K 0 1 B 0 1 = 3 частям, А 1 К 0 1 : К 0 1 В 0 1 =2: 3
Соединить точку В 0 1 с точкой В 1 и проведя из точки К 0 1 прямую параллельную (В 1 В 0 1) получим проекцию точки К 1 . Согласно теореме Фалеса (Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону, то на другой стороне отложатся равные между собой отрезки) А 1 К 1: К 1 В 1 = = 2: 3, далее находим К 2 . Таким образом проекции точки К делят одноименные проекции отрезка АВ в данном отношении следовательно и точка К делит отрезок АВ в отношении 2: 3.


6 ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА ПРЯМОЙ И УГЛОВ
НАКЛОНА ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ
Длину отрезка АВ
можно определить из прямоугольного треугольника АВС
,гдеA
С
=
A
1
B
1
, СB
=
DZ
, угол a
- угол наклона отрезка к плоскости П
1
. Для этого на эпюре (рис. 21) из точки B
1
под углом 90 проводим отрезок B
1
B
1
0
=
DZ
,
полученный в результате построений отрезок A
1
B
1
0
и будет натуральной величиной отрезка АВ
, а угол B
1
A
1
B
1
0
= α
. Рассмотренный метод называется методом прямоугольного треугольника
. Однако все построения можно объяснить, как вращение треугольника АВС
вокруг стороны AС
до тех пор, пока он не станет параллелен плоскости П
1
, в этом случае треугольник проецируется на плоскость проекций без искажения. Для определения b
- угла наклона отрезка к плоскости П
2
построения аналогичные (рис. 22). Только в треугольнике АВС
сторона ВС
=
D
U
и треугольник совмещается с плоскостью П
2
.
? Обозначить проекции прямой и
определить угол α.
Обозначить проекции прямой и
 определить угол α.
определить угол α.
Обозначить проекции прямой и
 определить угол β.
определить угол β.
7 ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ
Прямые в пространстве могут пересекаться, скрещиваться и быть параллельными.
1. Пересекающиеся прямые – это прямые, которые лежат в одной плоскости и имеют общую точку (a ∩ b = K ).
Теорема: Если в пространстве прямые пересекаются , то на чертеже пересекаются их одноименные проекции (рис. 23).
Т очка пересечения одноименных проекций находится на одном перпендикуляре к оси Х
(К
1 К
2 Ох
).
очка пересечения одноименных проекций находится на одном перпендикуляре к оси Х
(К
1 К
2 Ох
).
К = a ∩ b К a ; К b К 1 = a 1 ∩ b 1 ;
К
2 = a
2 ∩ b
2 .
Справедлива и обратная теорема:
Если К 1 а 1 ; К 2 b 2 , то
К 1 = а 1 ∩ b 1 ;
К
2 = а
2 ∩ b
2 К
= а
∩ b
.
2.
Скрещивающиеся прямые
– это прямые, которые не лежат в одной плоскости и не имеют общей точки (рис. 24).
Пары точек 1 и 2 , лежащие на горизонтально-проецирующей прямой называются горизонтально-конкурирующими, а точки 3 и 4 – фронтально-конкурирующими. По ним определяется видимость на эпюре.
П о горизонтально-конкурирующим точкам 1
и 2
определяется видимость относительно П 1 . Точка 1
ближе к глазу наблюдателя, она будет видима на плоскости П 1 . Так как точка 1 m
, то прямая m
будет выше прямой n
.
о горизонтально-конкурирующим точкам 1
и 2
определяется видимость относительно П 1 . Точка 1
ближе к глазу наблюдателя, она будет видима на плоскости П 1 . Так как точка 1 m
, то прямая m
будет выше прямой n
.
Какая прямая будет видимой по отношению к плоскости
П 2
?
3.
Параллельные прямые
– это прямые, которые лежат в одной плоскости и имеют несобственную общую точку.
Теорема:
Е сли в пространстве прямые параллельны, то на чертеже параллельны их одноименные проекции (рис. 25).
сли в пространстве прямые параллельны, то на чертеже параллельны их одноименные проекции (рис. 25).
Если k
m
k
1 m
1 , k
2 m
2 , k
3 m
3
Справедлива обратная теорема:
Если k
1 m
1 ; k
2 m
2 k
m
Лекция № 3
ПЛОСКОСТЬ
1. Способы задания плоскости на чертеже. Следы плоскости. 2. Положение плоскости относительно плоскостей проекций. 3. Принадлежность точки и прямой плоскости. 4. Главные (особые) линии плоскости.
1 СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЧЕРТЕЖЕ.
СЛЕД ПЛОСКОСТИ
Плоскость – бесконечная во все стороны линейчатая поверхность, которая на всем своем протяжении не имеет кривизны и преломления.
Плоскость на чертеже может быть задана:
Тремя точками, не лежащими на одной прямой – Р (A , B , C ) , рис. 26.
Прямой и точкой, не лежащей на этой прямой –Р (m , A ; A m ) , рис. 27.Рис. 29 Рис. 30
Задание плоскости следамиСлед плоскости – линия пересечения плоскости с плоскостью проекций (рис. 31).
Горизонтальный след получается при пересечении плоскости Р с горизонтальной плоскостью проекций (Р П1 = Р ∩ П 1).
Р П2 = Р ∩ П 2 – фронтальный след ;
Р
 П3 = Р ∩ П 3 – профильный след
;
П3 = Р ∩ П 3 – профильный след
; Р x , Р y , Р z – точки схода следов .

|
Положение точки |
Наглядное изображение |
Комплексный чертеж |
Характерные признаки |
|
принадлежит плоскости 1 |
|
А 1 – ниже оси Х, А 2 – на оси X |
|
|
принадлежит плоскости 1 |
|
|
B 1 – выше оси X, B 2 – на оси X |
|
принадлежит плоскости 2 |
|
|
С 2 – выше оси X, С 1 – на оси Х |
|
принадлежит плоскости 2 |
|
|
D 1 – на оси X, D 2 – ниже оси X |
|
принадлежит оси X |
|
E 1 совпадает с E 2 и принадлежит оси X |
Задача № 1.
Построить комплексный чертеж точки А, если:
точка расположена во II четверти и равноудалена от плоскостей 1 и 2 .
точка расположена в III четверти, и ее расстояние до плоскости 1 в два раза больше, чем до плоскости 2.
точка расположена в IV четверти, и ее расстояние до плоскости 1 больше, чем до плоскости 2 .
Задача № 2.
Определить, в каких четвертях расположены точки (рис. 2.21).

Задача № 3.
Построить наглядное изображение точек в четвертях:
а) А – общего положения в III четверти;
б) В – общего положения в IV четверти;
в) С – во второй четверти, если ее расстояние от 1 равно 0;
г) D – в I четверти, если ее расстояние от 2 равно 0.
Задача № 4.
Построить комплексный чертеж точек А, В, С, D (см. задачу 3).
§ 5. Система трех взаимно перпендикулярных плоскостей
На практике исследования и построения изображений система двух взаимно перпендикулярных плоскостей не всегда дает возможность однозначного решения. Так, например, если переместить точку А вдоль оси Х, то ее изображение не изменится.
Положение точки в пространстве (рис. 2.22) изменилось (рис. 2.24), а изображения на комплексном чертеже остались без изменений (рис. 2.23 и рис. 2.25).
|
|
|
|
|
|
Для решения данной задачи вводят систему трех взаимно перпендикулярных плоскостей, так как при составлении чертежей, например машин и их частей, требуется не два, а больше изображений. На этом основании в некоторые построения при решении задач необходимо вводить в систему 1 , 2 и другие плоскости проекций.
|
|
Рассмотрим три взаимно перпендикулярные плоскости 1 , 2 , 3 (рис. 2.26). Вертикальная плоскость 3 называется профильной плоскостью проекции. Пересекаясь между собой, плоскости 1 , 2 , 3 образуют оси проекций, при этом пространство делится на 8 октантов. 1 2 = x; -x 1 3 = у; -у 2 3 = z; -z 0 – точка пересечения осей проекций. |
Эти плоскости делят все пространство на VIII частей, которые называются октантами (от лат. okto восемь). Плоскости не имеют толщины, непрозрачны и бесконечны. Наблюдатель находится в первой четверти (для систем 1 , 2) или первого октанта (для систем 1 , 2 , 3) в бесконечном удалении от плоскостей проекций.
10.1 Двугранный угол. Угол между плоскостями
Две пересекающиеся прямые образуют две пары вертикальных углов. Подобно тому как две пересекающиеся прямые на плоскости образуют пару вертикальных углов (рис. 89, а), так две пересекающиеся плоскости в пространстве образуют две пары вертикальных двугранных углов (рис. 89, б).
Рис. 89
Двугранным углом называют фигуру, которая состоит из двух полуплоскостей, имеющих общую граничную прямую и не лежащих в одной плоскости (рис. 90). Сами полуплоскости называют гранями двугранного угла, а их общую граничную прямую - его ребром.

Рис. 90
Измеряют двугранные углы следующим образом.
Возьмём на ребре р двугранного угла с гранями α и β точку О. Проведём из точки О в его гранях лучи а и Ь, перпендикулярные ребру р: а - в грани α и b - в грани β (рис. 91, а).

Рис. 91
Угол со сторонами а, b называется линейным углом двугранного угла.
Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла.
Действительно, возьмём другую точку О 1 ребра р и проведём в гранях α и β лучи а 1 ⊥ р и b 1 ⊥ р (рис. 91, б).
Отложим на луче а отрезок ОА, на луче а 1 отрезок O 1 A 1 , равный отрезку ОА, на луче b отрезок ОВ и на луче b 1 отрезок О 1 В 1 , равный отрезку ОВ (рис. 91, в).
В прямоугольниках ОАА 1 О 1 и 0ВВ 1 0 1 стороны АА 1 и ВВ 1 равны их общей стороне ОО 1 и параллельны ей. Поэтому АА 1 = ВВ 1 и АА 1 || ВВ 1 .
Следовательно, четырёхугольник АВВ 1 А 1 - параллелограмм (рис. 91, г), а значит, АВ = А 1 В 1 . Поэтому треугольники АВО и А 1 В 1 O 1 равны (по трём сторонам) и угол ab равен углу a 1 b 1 .
Теперь можно дать такое определение: величиной двугранного угла называется величина его линейного угла.
Углом между пересекающимися плоскостями называется величина меньшего из образованных ими двугранных углов. Если этот угол равен 90°, то плоскости называются взаимно перпендикулярными. Угол между параллельными плоскостями полагается равным 0°.
Угол между плоскостями α и β, как и величина двугранного угла с гранями α и β, обозначается ∠αβ.
Угол между гранями многогранника, имеющими общее ребро, - это величина соответствующего этим граням двугранного угла.
10.2 Свойства взаимно перпендикулярных плоскостей
Свойство 1 . Прямая, лежащая в одной из двух взаимно перпендикулярных плоскостей и перпендикулярная их общей прямой, перпендикулярна другой плоскости.
Доказательство. Пусть плоскости α и β взаимно перпендикулярны и пересекаются по прямой с. Пусть прямая а лежит в плоскости α и a ⊥ с (рис. 92). Прямая а пересекает с в некоторой точке О. Проведём в плоскости β через точку О прямую Ь, перпендикулярную прямой с. Так как α ⊥ β, то a ⊥ b. Так как a ⊥ b и a ⊥ с, то α ⊥ β по признаку перпендикулярности прямой и плоскости.

Рис. 92
Второе свойство является утверждением, обратным первому свойству.
Свойство 2 . Прямая, имеющая общую точку с одной из двух взаимно перпендикулярных плоскостей и перпендикулярная другой плоскости, лежит в первой из них.
Доказательство. Пусть плоскости α и β взаимно перпендикулярны и пересекаются по прямой с, прямая a ⊥ β и а имеет с а общую точку А (рис. 93). Через точку А проведём в плоскости α прямую р, перпендикулярную прямой с. Согласно свойству 1 р ⊥ β. Прямые а и р проходят через точку А и перпендикулярны плоскости β. Поэтому они совпадают, так как через точку проходит лишь одна прямая, перпендикулярная некоторой плоскости. Поскольку прямая р лежит в плоскости α, то и прямая а лежит в плоскости α.

Рис. 93
Следствием свойства 2 является такой признак перпендикулярности прямой и плоскости: если две плоскости, перпендикулярные третьей плоскости, пересекаются, то прямая их пересечения перпендикулярна третьей плоскости.
Доказательство. Пусть две плоскости α и β, пересекающиеся по прямой а, перпендикулярны плоскости γ (рис. 94). Тогда через любую точку прямой а проведём прямую, перпендикулярную плоскости γ. Согласно свойству 2 эта прямая лежит и в плоскости α, и в плоскости β, т. е. совпадает с прямой а. Итак, а ⊥ γ.

Рис. 94
10.3 Признак перпендикулярности плоскостей
Начнём с практических примеров. Плоскость двери, навешенной на перпендикулярный полу косяк, перпендикулярна плоскости пола при любых положениях двери (рис. 95). Когда хотят проверить, вертикально ли установлена плоская поверхность (стена, забор и т. п.), то это делают с помощью отвеса - верёвки с грузом. Отвес всегда направлен вертикально, и стена стоит вертикально, если отвес, располагаясь вдоль неё, не отклоняется. Эти примеры подсказывают нам следующий простой признак перпендикулярности плоскостей: если плоскость проходит через перпендикуляр к другой плоскости, то эти плоскости взаимно перпендикулярны.

Рис. 95
Доказательство. Пусть плоскость α содержит прямую а, перпендикулярную плоскости β (см. рис. 92). Тогда прямая а пересекает плоскость β в некоторой точке О. Точка О лежит на прямой с, по которой пересекаются плоскости α и β. Проведём в плоскости β через точку О прямую b, перпендикулярную прямой с. Так как a ⊥ β, то a ⊥ b и a ⊥ с. Это означает, что линейные углы двугранных углов, образованных пересекающимися плоскостями α и β, - прямые. Поэтому плоскости α и β взаимно перпендикулярны.
Отметим, что каждые две из трёх прямых а, b и с, рассмотренных сейчас (см. рис. 92), взаимно перпендикулярны. Если же построить ещё одну прямую, проходящую через точку О и перпендикулярную двум из этих трёх прямых, то она совпадёт с третьей прямой. Этот факт говорит о трёхмерности окружающего нас пространства: четвёртой прямой, перпендикулярной каждой из прямых а, b и с, нет.
Вопросы для самоконтроля
- Как вычисляют величину двугранного угла?
- Как вычислить угол между плоскостями?
- Какие плоскости называются взаимно перпендикулярными?
- Какие свойства взаимно перпендикулярных плоскостей вы знаете?
- Какой признак перпендикулярности плоскостей вы знаете?